|
 |
 |
 |
 |
||||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
 |
|||||||||
Bookkeeping today is done with computers. If the input is correct, the output (answer) will be correct and will be figured at the speed of light, which is really, really fast, so there is no longer any justification in being tied to the old ways of adding, subtracting, multiplying, and dividing. In today’s high-tech society, when adults want an answer to an arithmetic problem, they use a calculator, and unless something better comes along, that is what today’s children will do when they are adults.
The purpose in teaching algorithms today is to develop an understanding of the four operations (ASMD), illustrate how a number system works, and build confidence in working with numbers. Although our society is high-tech, children’s minds are low-tech (in spite of the dexterity with which they play electronic games), and to bridge the gap, we must start with the children where they are, not where we want them to be.
Ideally, an algorithm should be easy to learn, non-stressful, reduce almost to zero the likelihood of making a careless or mental mistake, and diagnostic in revealing the where-abouts of mistakes if made. Only , , and meet all of these criteria and are therefore the algorithms of choice for addition and multiplication in ALL KIDS CAN LEARN ARITHMETIC. In contrast, the stan-dard ways to add and multiply do not meet any of the criteria and are not taught in the program except as other ways to add and multiply and how most adults, including you, probably, were taught to add and multiply.
Monster Addition
Monster Addition is an amazingly powerful algorithm. It is attributed to who called it the Addition Facts Algorithm to indicate that its only prerequisite is competence with the addition facts. We call it Monster Addition because of the monstrous addition problems that are easily worked with it.
YouTube video: x (1:41)
YouTube video: (3:06)
YouTube video: (2:03)
Children in kindergarten, grade 1, and grade 2 should be taught how to import (add) in different lands (bases) as explained on page 5 before being taught the Monster Addition algorithm; otherwise, they will not understand why it works. In contrast, children in grades 3, 4, 5, and 6 should be taught the algorithm straightaway, even if rotely, to stifle a debilitating mindset that develops in grades 1, 2, and 3—that of “always carrying a 1.”
Monster Addition Breaks the Habit of Always “Always Carrying a 1”
The mindset of “always carrying a 1” occurs when, for years, children add just two numbers at a time. With hardly any exceptions, they do just that for all of grade 1, 2, and 3 in every major elementary school math program in America today, but look what happens in adding just two numbers: The biggest sum one gets in any column is 19, so if anything is “carried,” it will always be a 1, thus the mindset to “always carry a 1.”
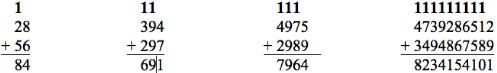
The frequency and persistence of the mindset of “always carrying a 1” is revealed in pre-senting elementary school children with the two addition problems below, the first one to see if they know how to add three numbers in a column, the second one (shown twice) to test for the mindset. The correct answer for the first one is 67, that for the second one 91. An answer of 82 for the second one reveals the mindset resulting from 6+8+7=21, “put down the 2 and carry the 1.”
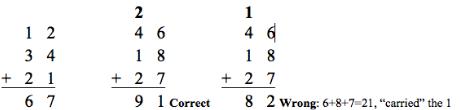
CONTINUED: Next > | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | < Back
Ten Land (Base Ten) Addition & Subtraction Activities
Hands-on addition and subtraction activities with Ten Land (base 10) blocks. Addition is modeled as an importing even, subtraction as an exporting event. Sequences from no recording to recording just answers to recording all trades and answers. Includes answers.
Grades K-6, 72 pages. Best used over several grades
Available only from this website.