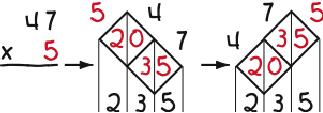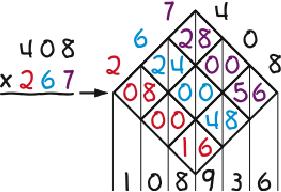
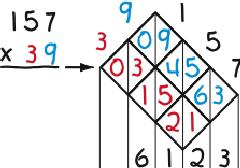
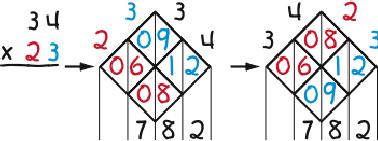
Lattice Multiplication is a derivative of Napier’s “bones”—the first calculator: numbered rods for multiplying and dividing created by John Napier, a Scottish mathematician, in the early 1600s. To replicate the rods, (1) draw a lattice with as many diagonal rows and columns as are needed to allow writing the problem across the top of the lattice, one digit per row or column, (2) split the cells in the lattice with vertical lines, (3) fill in the cells with the products of the digits at the ends of the intersecting rows and columns, inserting zeros as needed to fill in both sides of the cells, and (4) add the numbers between the vertical lines that result. The examples below illustrate the process. The first two are worked twice to show that it doesn’t matter if the multiplier is written first or second.

The most striking feature of Lattice Multiplication is that it separates the multiplication from the addition in first filling in the lattice and then adding the contents. Compare that to how the operations are mixed in —the conventional multiplication algorithm. Also noteworthy is that it is easily learned, keeps work organized, is non-stressful (because it allows a user to take a break anywhere in a problem and pick up later where he or she left off), and is diagnostic in that it shows where in a problem things went wrong in the event of a wrong answer. Its biggest drawback is having to draw the lattice. A teacher tip in that regard is to turn one’s paper about 45 degrees, draw the lattice straight up and down and across, and then turn one’s paper back.

Next > | Lattice Multiplication | Blank Lattices |