
Figuring Out the Division Facts
Prerequisites: The Tap & Tally™ numerals and knowing how to skip count by 2s to 20 (2-4-6- ... -20), 3s to 30 (3-6-9- ... -30), 4s to 40 (4-8-12- ... -40), and so on up to the 10s to 100 (10-20-30- ... -100), the same as for the multiplication facts.
The program designates the division facts for the 2s, 5s, and 10s beginning in Kinder-garten; those for the 3s and 4s beginning in Grade 1; and those for the 6s, 7s, 8s, and 9s beginning in Grade 2, the same as for the multiplication facts.
Procedure: Think, “How many divisors are in the dividend?” Then, skip count by the divisor up to the dividend, keeping track of the counts with tally marks. The number of counts is the quotient.
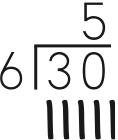
Note that the procedure does not employ the Tap & Tally™ numerals, only skip counting and tally marks. Also note that the skip counting is forward, the same as for multiplication.
Remarks: The division facts have traditionally been taught as “gazintas” in elementary school math: “How many times does the divisor gazinta (goes into) the dividend?” A student is to guess the answer and multiply the guess by the divisor to see if the product equals the dividend. If it does, the guess was correct. For 20÷4, 4 gazinta 20 five times, and 5 is the answer because 4x5=20. Note that the process does not rely on the meaning of division. In Tap & Tally™, there is no guessing and division is meaningful. For 20÷4, the number of 4s in 20 is determined by a direct count: 4-8-16-20-24 for five 4s.
Tap & Tally™ Lessons 41-48
For 30 ÷ 6, think “How many 6s are in 30?” Answer by skip counting by 6 and keeping track of the counts with tally marks for an answer of 5, the number of counts: 6 (/), 12 (//), 18 (///), 24 (////), 30 (/////).
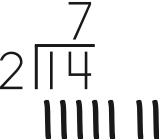
For 14 ÷ 2, think “How many 2s are in 14?” Answer by skip counting by 2 and keeping track of the counts with tally marks for an answer of 7, the number of counts: 2 (/), 4 (//), 6 (///), 8 (////), 10 (/////), 12 (//////), 14 (///////).
Mad Minute Primer