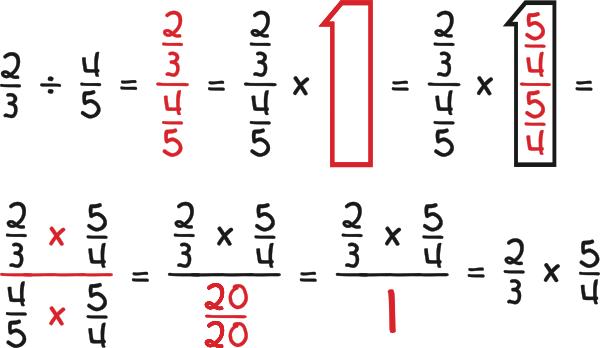Mr. Novak’s Proof

Mr. Novak’s proof of the mysterious “invert and multiply” rule for fractions is shown below for 2/3 ÷ 4/5. By substituting letters for the numbers, such as “a” for 2, “b” for 3 (b ≠ 0), “c” for 4, and “d” for 5 (d ≠ 0), the rule is established for all fractions.

The proof rests on special properties of the number 1:

•xAny number times 1 is that number (N x 1 = 1 x N = N for all N).

•xAny non-zero number divided by itself is 1 (N ÷ N = N/N =1 for all N ≠ 0).

•xAny number divided by 1 is that number (N ÷ 1 = N/1 = N for all N).

Avoidance behavior drives the proof: Why divide by a “hideous” fraction like 4/5 when dividing by 1 would be so much easier? Thus the proof amounts to pulling a rabbit out of a hat to divide by 1 by multiplying the divisor 4/5 by its reciprocal 5/4 to turn it into 1.