 |
 |
 |
 |
 |
||||||||||
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||

• Finally, have them figure out what to do with the numbers in the problem to get the answer they got with the pictures. Since they figured out what to do before, they can usually figure out what to do again, but more quickly.
To illustrate, let’s pretend that we are the person with the thought balloon at the start of this key wondering if it matters which fraction to invert in dividing fractions. Maybe we have been presented with a problem like 23/87 ÷ 161/194, and the sheer “ugliness” of it zapped the rule right out of our heads. We at least remember that we have to turn one of the fractions upside down before we multiply across, but we are not sure if it is the first one or the second one or if it matters. So let’s make up a simple problem like the nasty one, like 1/2 ÷ 1/4, that we could solve with the Fraction Circles and draw pictures of 1/2 and 1/4.
• Then have them make up a simple problem like the one they are trying to solve and solve it by drawing pictures of the Fraction Circles.
Reasoning that 1/2 ÷ 1/4 asks the same question as 10 ÷ 2 (How many 2s in 10?), we know 1/2 ÷ 1/4 = 2 because we can see that two quarters (green sections) answer the question “How many fourths in a half?” We then see that it does matter as to which number to invert in dividing fractions, because if we invert the first one, as below, we get 1/2 instead of 2. The rule is thus to invert the second one, namely, the divisor.
Inverting first fraction: 1/2 ÷ 1/4 “=” 2/1 x 1/4 = 2x1/1x4 = 2/4 = 1/2 WRONG! However, if we inverted the result, 1/2, we’d get the right answer, so we could make up a “double” invert rule: Invert the first one (the dividend), multiply across, and invert the result.
Inverting second fraction: 1/2 ÷ 1/4 “=” 1/2 X 4/1 = 1x4/2x1 = 4/2 = 2 RIGHT!!!
Fractions are Forever
Everyday, millions, billions, and trillions of computations are performed worldwide by calculators and computers. Virtually all of them are performed with whole numbers and decimals, not fractions. So will fractions someday become obsolete? No. Not ever! Even if someday people are accustomed to asking for “point five” of a sandwich instead of half of one, fractions are too embedded in math to go away.
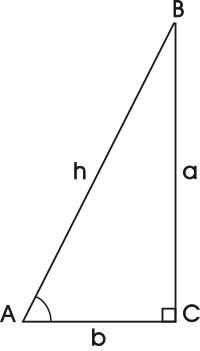
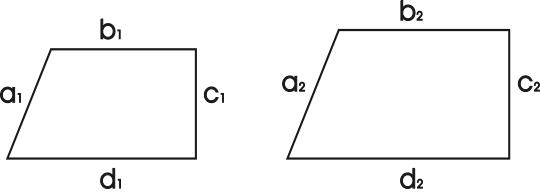
In algebra, if 7x = 11, then x = 11/7. In geometry, if figures are similar, then their corresponding parts are in proportion (a1/a2 = b1/b2 = c1/c2 = d1/d2). In , the likelihood of getting a head when tossing a fair coin is 1/2. In trigonometry, for a right triangle with sides a and b and hypotenuse h, SinA = a/h, CosA = b/h, and TanA = a/b. In calculus, the derivative of y with respect to x is dy/dx.
Math Games & Activities, Vol. 2
Eighty games, activities, worksheets, and instructional aids for all major topics in number, geometry, and measurement in elementary school math. Diagnostic/prescriptive games for whole numbers, fractions, decimals, and percent. A complete program for teaching understanding of arithmetic word problems based on viewing addition, subtraction, multiplication, and division as combining and separating actions.
Answers and more than 100 pages of instructions with lots of examples and illustrations.
Grades 4-9, 322 pages with permission to duplicate.
FOCUS on Pre-Algebra
A sensible approach to teaching beginning algebra.
Instead of memorizing the rules for working with integers or signed numbers, students discover the rules by manipulating colored counters and noting the patterns that ensue, alnd instead of working with algebraic expressions solely in the abstract, they make sense out of them with algebra tiles and work them concretely.
Grades K-9, 48 pages with permission to duplicate.




