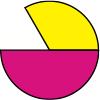
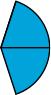
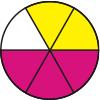
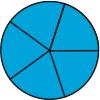
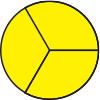
Seeing that 1/2 = 3/6 and 1/3 = 2/6, we see that the answer is 5/6, but why sixths? Why not some other fraction, like fourths or tenths? Real fractions show why.

What works is a magic show to the novice. The circles are put back together, and the first two are cut into sixths.

If one of the halves is placed next to one of the thirds (to indicate that they are being added) and compared to two of the fifths, then it is visually clear that the answer has to be bigger than 2/5, so adding across does not work.

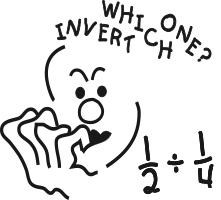
The rules for working with fractions don’t make sense to elementary school students if they only work with the numbers. What the numbers prompt them to do is often wrong. Take 1/2 + 1/3, for example. What is wrong with just adding across and getting 2/5? Lots, but that isn't obvious unless real fractions are considered, like three circles—one cut into halves, one into thirds, and one into fifths.

CONTINUED: Next > | 1 | 2 | 3 | 4 | 5 | 6 | 7 |

Think Links: Fractions • Decimals • Percent

Teaching and maintenance activities on fraction-decimal-percent equivalences in a game-like format. Presents decimals and percent as simply other ways of writing, thinking, and talking about the same thing: fractions. Answers to hundreds of equivalences in the activities themselves. Lots of pictures of fractional parts of squares that can be modeled with base 10 blocks to show the connection between fractions, decimals, and percent.

Ideal for small groups and learning centers.

Grades 1-6, 51 pages of reproducible black-line masters with permission to duplicate.

Available only from this website.