 |
 |
 |
 |
 |
||||||||||
 |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
 |
|||||||||||||
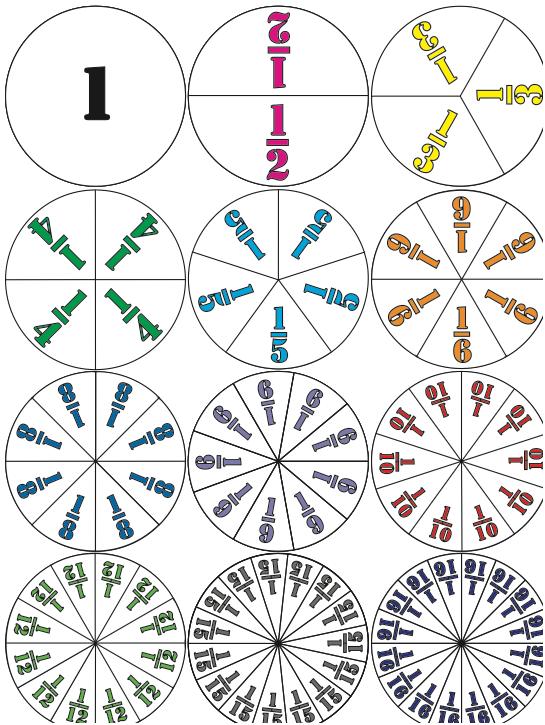

Teaching ASMD of Fractions to Elementary School Students
The goal in teaching ASMD of fractions with Fraction Circles is to teach students that they can figure out the rules themselves so they don’t have to rely on remembering them if they are not sure of one. All they have to remember is that they figured it out before, so they should be able to figure it out again. The teaching strategy for all four operations is the same:
• Students ASMD fractions with Fraction Circles to obtain answers that they know are correct because they can see that they are.
• They then examine the numbers in the problems they solved and the numbers in their answers to find a rule to get their answers using just the numbers in the problems. Usually, they can do this because the problems in the lessons are sequenced to make the rule stand out.
To “remember after forgetting,” students replicate these steps except with pictures they draw of Fraction Circles. An example of doing so for the “Ours is not to reason why ...” rule at the start of this key will be given later.
Adding and Subtracting Fractions with Fraction Circles
Adding or subtracting fractions is easy if the denominators are the same: just add or subtract the numerators. For example, 1/3+1/3=2/3 and 4/5-1/5=3/5. When the denominators aren’t the same, then they must be made the same, which gets us back to “easy.” However, how to make them the same requires thinking.
The “ideal” denominator for adding or subtracting fractions is called the “least common denominator” (LCD). It’s the smallest denominator that can be used. It is the “best” in terms of keeping the numbers small and maybe not having to reduce an answer, but it is the worst if required. Requiring it adds needless and debilitating stress. If students stumble across it, fine, but any common denominator will yield the same answer, so there is no need to insist on the LCD in adding and subtracting fractions.
The following lessons for adding and subtracting fractions are sequenced from “easy” to “thoughtful” to “doubly thoughtful.” They are self-explanatory and thus reasonably easy to direct. Use your judgment on how many problems students must work with the Fraction Circles before using just the numbers.
Adding Fractions with Fraction Circles
•
•
•
Subtracting Fractions with Fraction Circles
•
•
•
Butterfly Fractions
is a derivative of “cross” multiplication for adding and subtracting fractions. It is easy to use and, because of the goofy picture that it is based on, easy to remember. Depending on the age of the students, it may be taught before the work with the Fraction Circles. For older students about to be tested on fractions with some standardized test, it is a good thing for them to know before the test to avoid being humiliated. Afterwards, though, they should complete the lessons for adding and subtracting fractions with Fraction Circles so they learn how to think about fractions.





