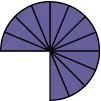
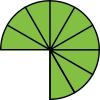
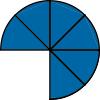
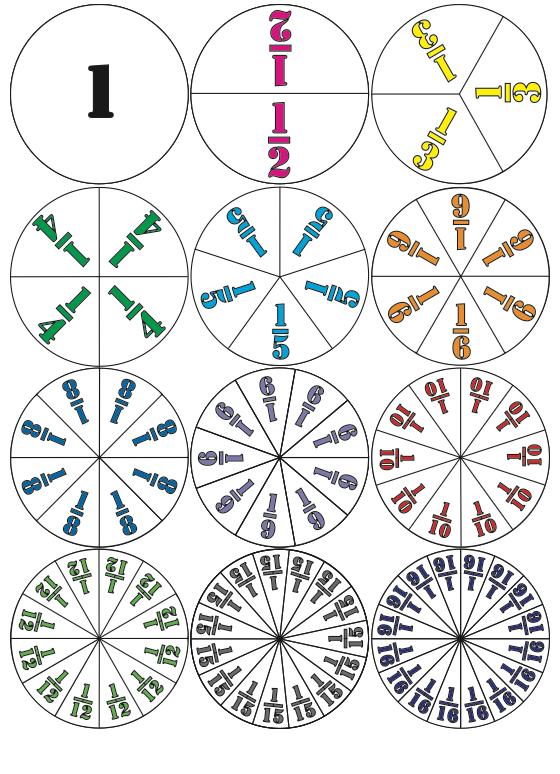
been divided into sixths (5/6), five pieces of the Fraction Circle that has been divided into eighths (5/8), and five pieces of the Fraction Circle that has been divided into tenths (5/10). Ask students to describe what happens as the denominator gets bigger. (The fraction gets smaller, which is not obvious without the Fraction Circles.) Follow with for the numerator 1.

To emphasize the meaning of the numerator—that it determines the number of pieces—do the reverse: Keep the denominator constant and hold up fractions like one of the pieces of the Fraction Circle that has been cut into fourths (1/4), then three of the pieces (3/4), and then four of the pieces (4/4). Ask students to describe what happens as the numerator gets bigger. (The fraction gets bigger.) Follow with (for denominators 2 and 10), , and .

For review and practice, play every so often. It doesn’t take long to play. Like regular Tic-Tac-Toe, the objective is to get three in a row horizontally, vertically, or diagonally. To extend the game after someone wins, play for four corners, the minus sign (three Xs straight across the middle, the equal sign (three Xs straight across the top and three straight across the bottom), the plus sign (three Xs straight across the middle and three straight down the middle), and Blackout (Xs everywhere).

Teaching Equivalent Fractions with Fraction Circles

Begin with a fraction that has lots of equivalences like 3/4 and ask students to find as many “fair trades” (like in Fair Lands™) with the Fraction Circles as they can for the fraction and to record their findings as fractions from “lowest terms” (smallest numbers) to “greatest terms” (biggest numbers). Remind them of the one caveat for the Fraction Circles—no mixing of colors, that is, denominators—which means for 3/4 that they can’t, for example, trade two of the fourths (2/4) for one of the halves (1/2) and the remaining fourth (1/4) for two of the eighths (2/8). They can, however, trade all three of the fourths (3/4) for six of the eighths (6/8), nine of the twelfths (9/12), and twelve of the sixteenths (12/16). When finished, they can see that 3/4 = 6/8 = 9/12 = 12/16 as shown below.

• Ask students to describe the number patterns in their list of equivalences for 3/4. (The numerators are the skip counting numbers for 3, the denominators those for 4.)

• Ask them to use the number patterns to extend their list of equivalences out to 10 fractions (to 30/40). Ask them what the last fraction would be if they extended their list out to 20 fractions (60/80). Out to 50 fractions (150/200). Out to 100 fractions (300/400).

CONTINUED: Next > | 1 | 2 | 3 | 4 | 5 | 6 | 7 | < Back

Real Fractions

A booklet of 17 guided discovery activities for the fraction circles.

FREE e-book! Download only from this website.

Fraction Circles

Needed to teach fractions effectively to elementary school students. Fraction rules do not make sense unless.one can picture fractional parts of things in their mind. Among the models for fractions, circles are the best because the unit is always evident: half a pie is half a pie no matter the size of the pie. In contrast, the unit for rods, squares, or rectangles is arbitrary. For instance, for the Cuisenaire rods, if the purple or 4-rod is the unit, the red or 2-rod is 1/2, but if later the orange or 10-rod is the unit, it is 1/5.

FREE e-book! Download only from this website.