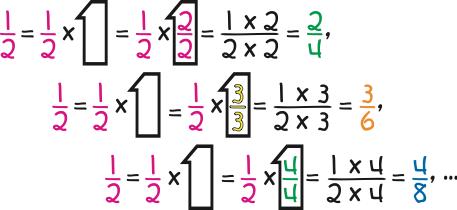|
 |
 |
 |
 |
||||||||||
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
 |
|||||||||||
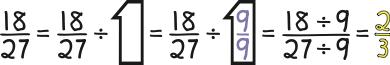
• Tell students that one of the fractions is “reduced.” Ask them which one and why. (Don’t tell them. Let them think about it, not try to remember what you tell them. There is too much to know in math to try to commit it all to memory. A surer and shorter road to success in math is to become a thinker, not a rememberer.)
• Have them name five more fractions that would reduce to 1/2.
Repeat for other fractions like 12/16, 8/12, and, 6/10 that can be reduced. Follow with .
A fraction can be reduced if both its numerator and denominator can be divided by the same number. In reducing it, the number 1 as N/N is being divided out or “canceled” as shown below. Since dividing a number by 1 doesn’t change the value of a number, the result is the same fraction except with smaller numbers.

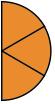
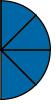
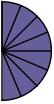
This property of the number 1 as N/N to morph fractions into their equivalents is the basis for the admonition that one may multiply both top and bottom of a fraction by the same number without changing the value of the fraction.
Teaching Reducing Fractions to Elementary School Students
Begin with a fraction that can be reduced like 8/16 and ask students to again find as many fair trades with the Fraction Circles as they can for the fraction and to record them from “greatest terms” (biggest numbers) to “lowest terms” (smallest terms). Remind them that they can’t mix colors (denominators), which means for 8/16 that they can’t, for example, trade four of the sixteenths for one of the fourths (1/4) and four of them for two of the eighths (2/8). They can, however, trade all eight of them for six of the twelfths (6/12), five of the tenths (5/10), four of the eighths (4/8), three of the sixths (3/6), two of the fourths (2/4), and one of the halves (1/2). When finished, they can see that 8/16 = 6/12 = 5/10 = 4/8 = 3/6 = 2/4 = 1/2 as shown below.
Repeat for other fractions like 1,2, 2/3, and 3/5. Follow with and . For review and practice, play .
The overarching principle with equivalent fractions is that they are the “same but different”—the same in quantity but different in appearance. They are the product of the number 1 of the form N/N as shown below for equivalences of 1/2.