The notation for a fraction, that M slash N (M/N) means M parts of something cut into N equal parts—that 7/12 means 7 parts of something cut into twelfths, for example—communicates concisely and precisely how much of something is being considered. Take 1/2 of a banana, for example. The notation refers to one banana that is cut into two pieces that are about the same size. Even young children grasp the meaning of the notation. They certainly have no more problem with the notation for 1/2 a banana, 1/6 of a pie, or 1/8 of a pizza than they do with the “notation” or spelling of the words they are learning to read, which is why they should be taught fraction notation right along with reading before they think fractions are just for grownups and thus harder to learn than they are.

The main reason American students are behind their foreign counterparts in math is that they are protected from it. The prevailing mindset in American education is that math is too abstract for children. Baloney! Language is pure abstraction with lots of rules (grammar), and all children are actively engaged in learning everything they hear from the moment they are born. If they grow up in a bilingual home, they will speak both languages—without an accent—by the time they are old enough to attend school. Frightening is that the older they get, the harder it will be for them to learn other languages. Math is a language for interpreting quantitative events. For children to be fluent in it—to speak it without an accent—they need to experience it right along with the other languages they are learning. The longer it is kept from them, the harder it will be for them to learn it when they are older.

To teach fractions effectively to students of any age, even adults, assume that your students will eventuallyforget every rule you teach them. They may remember the rules for a test, but most will not remember them long after the test. That is bound to happen once the rules are no longer being practiced on a regular basis. The use it or lose it maxim cannot be denied. Teachers who ignore the propensity for students to forget are simply being unrealistic. So to teach fractions effectively, do not teach the rules. Instead, teach how to figure out the rules with real fractions—the for this key. Then when students forget the rules, they can recreate them when needed by figuring them out again like they did with the Fraction Circles. Since they figured them out before, they know they can figure them out again.

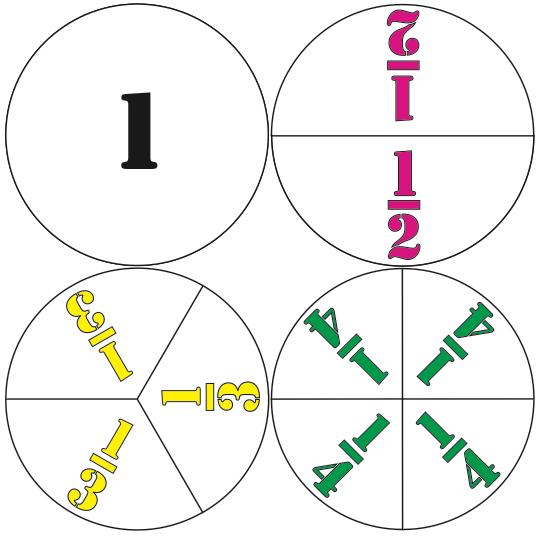
Teaching Fraction Notation with Fraction Circles

Begin by having students play with the fraction circles until they understand the notation on them, that 1/8, for example, refers to one of the slices of a circle cut into 8 equal slices. Emphasize that the slices must be equal—that they cannot be just any eight slices no matter how the circle is sliced. Then extend to combinations of the slices for a particular fraction circle, like three of the 1/8 slices. A proven strategy for doing so is to challenge your students to show 3/8 by holding up three of the 1/8 slices.

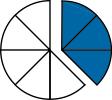
Repeat with other fractions until you are certain they can “read” fractions. Then reverse the activity. Hold up, say, seven of the pieces of the fraction circle that has been cut into twelfths (7/12), and have students write the fraction being illustrated.

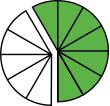
To emphasize that the bottom number (denominator) of a fraction determines the "size" of a fraction, hold up fractions with the same top number (numerator) but different bottom numbers like five pieces of the fraction circle that has

CONTINUED: Next > | 1 | 2 | 3 | 4 | 5 | 6 | 7 | < Back